鉛直ブレースの断面算定は、どのように行われているのでしょうか。
まずは例題です。
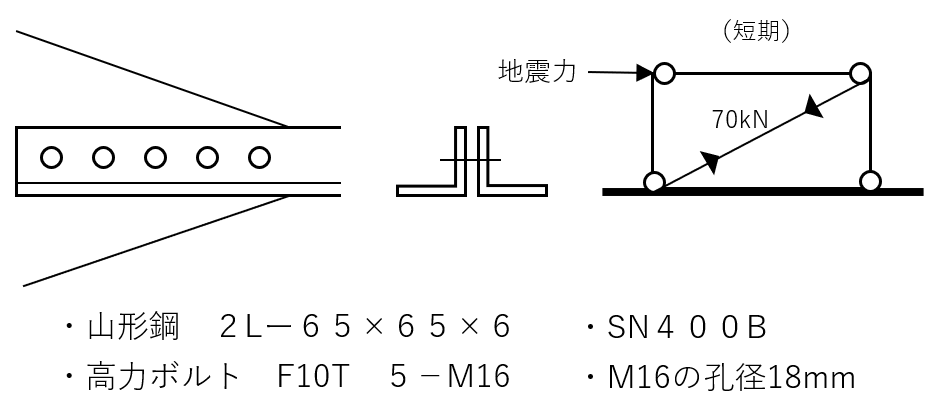
答えは、こちらです。
解説していきます。
本問をみると、ブレースに引張応力が働いています。
そのため下式①で、引張応力を求め、引張許容応力度以下であることを確認する必要があります。
ブレースの引張許容応力度σt = N / A = 70×1000/1289.4 = 54.3N/㎟
鉛直ブレースの有効断面積Aについて、
鉛直ブレース(2L-65×65×6)の断面積は、鋼構造設計基準によると7.527㎠/本です。
本問は、”２面摩擦”、”孔径18mm”であることを考慮して有効断面積Aを求めると下記の通りです。
ブレースの有効断面積A = 断面積×単位調整×鋼材の本数ー孔径×鋼材の厚み×鋼材の本数
(山形鋼の場合) = 7.527×100×2ー18×6×2 = 1289.4㎟
有効断面積Ａの算出には、高力ボルト孔を差し引く必要があります。
(下図の斜線部の面積を求めます。)
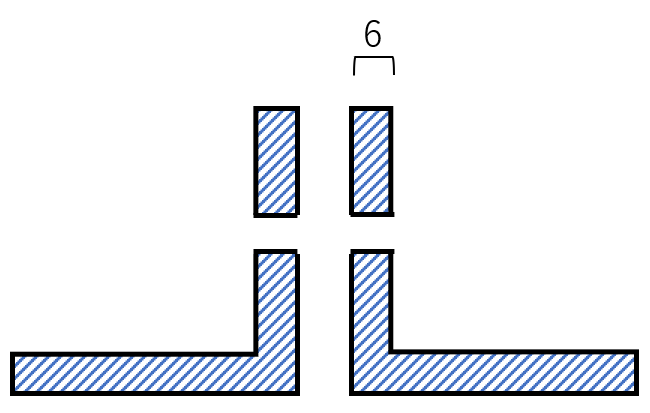
そして鋼構造設計基準によると、鉛直ブレースの材料SN400Bの許容引張応力度ftは、235N/㎟です。
そのため下記の通りの結果となり、鉛直ブレースは短期時において降伏しないことがわかります。
σｔ＜ｆｔ（54.3＜235）・・・ＯＫ
以下、補足です。（接合部の検討をしています。）
鉛直ブレースは、接合部を介して引張応力を負担しています。
鉛直ブレースが降伏するよりも早く接合部が破断しては、鉛直ブレースの機能を満足に発揮させることができないため高力ボルトに加わるせん断力が、高力ボルトの許容せん断耐力以下であることを確認する必要があります。
Ｆ１０Ｔ Ｍ１６の高力ボルトの許容せん断力＝90.5kN/本 です。
高力ボルトは５本のため高力ボルトの許容せん断力Qaは、下記の通りになります。
高力ボルトの許容せん断力Qa = 90.5×5 = 452.5kN
また本問の高力ボルトに作用するせん断力は、70kNであるため
高力ボルトＱａ＞許容せん断力（452.5＞70）・・・ＯＫ
となり、短期時において接合部も破断しないことがわかりました。
高力ボルトについて、もう少し解説した記事は、こちらです。
コメント